TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

 

 RELATIVIDADE DIMENSIONAL GRACELI.

 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

A histerese é a tendência de um sistema de conservar suas propriedades na ausência de um estímulo que as gerou, ou ainda, é a capacidade de preservar uma deformação efetuada por um estímulo. Podem-se encontrar diferentes manifestações desse fenômeno. A histerese mais conhecida ocorre no magnetismo^[1], mas também pode ocorrer em diversas áreas como mecânica clássica^[2], tráfego^[3], biologia^[4], epidemiologia^[5] entre outras^[6][7]. A palavra "histerese" deriva do grego antigo υστέρησις, que significa 'retardo', que foi cunhada por James Alfred Ewing em 1890.

Índice

• 1Saturação magnética
  • 1.1Inconveniente da saturação
  • 1.2Histerese magnética
  • 1.3Exemplo de histerese com metais
• 2Eletrônica
• 3Referências

Saturação magnética

Quando um campo magnético ${\displaystyle {\vec {H}}}$ (ampere-espira por metro) é aplicado a um material ferromagnético, passa a circular neste uma densidade de fluxo magnética (ou indução magnética) ${\displaystyle {\vec {B}}}$ (tesla = weber por metro quadrado). A relação entre densidade de fluxo e campo magnético é dada pela expressão ${\displaystyle {\vec {B}}=\mu {\vec {H}}}$^[8].

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Para uma geometria fixa, como o caso de uma bobina com núcleo fixo ou transformador, uma variação do campo magnético ${\displaystyle {\vec {H}}}$ é dada por uma variação na corrente da bobina que está sendo alimentada. Quanto maior a corrente ${\displaystyle I\,({\rm {{A})}}}$, maior o campo magnético ${\displaystyle {\vec {H}}\,({\rm {{A/m})}}}$^[9].

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Na região magnética linear ${\displaystyle {\vec {B}}=\mu {\vec {H}}}$ com ${\displaystyle \mu }$ constante (e da ordem de ${\displaystyle 1000\mu _{0}}$ ou mais), contudo, à medida que o campo magnético cresce, o material entra em uma região não linear (saturação magnética), onde ${\displaystyle \mu }$ passa a diminuir à medida que a saturação cresce.

Inconveniente da saturação

Quando atingida a saturação o transformador, mesmo a vazio, passa a demandar correntes maiores para manter o fluxo magnético imposto pela tensão. A relação entre fluxo magnético e tensão induzida é dada pela Lei de Faraday^[10]. Uma das formas de expressá-la é por ${\displaystyle \varepsilon =-n{\frac {{\text{d}}\phi }{{\text{d}}t}}}$, onde ${\displaystyle \phi }$ é o fluxo magnético, ${\displaystyle t}$ é o tempo , ${\displaystyle n}$ o número de espiras e ${\displaystyle \varepsilon }$ é a tensão induzida. Para simplificar a análise (e sem prejuízo de conceitos) consideraremos a tensão induzida no primário igual a tensão aplicada pela fonte.

Imaginando uma tensão de entrada sinusoidal ${\displaystyle v\left(t\right)={{v}_{0}}\sin \left(\omega t\right)}$, o fluxo demandado pelo núcleo do transformador será dado por ${\displaystyle \phi =-{\frac {1}{n}}\int {v\left(t\right)\,\,{\text{d}}t}={\frac {1}{n}}\omega {{v}_{0}}\cos \left(\omega t\right)}$,

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 ou seja, o fluxo é diretamente proporcional a tensão e a frequência de entrada. Trabalhando mais um pouco, pode-se chegar a expressão que o fluxo de pico de um sinal sinusoidal é dado por ${\displaystyle {{\phi }_{p}}={\frac {v_{rms}}{{\sqrt {2}}\pi nf}}}$, onde ${\displaystyle f}$ é a frequência em hertz.

A densidade de fluxo que atenda ao fluxo demandado é dada pela relação ${\displaystyle B={\frac {\phi }{A}}}$, onde ${\displaystyle A}$ é a área da secção transversal à passagem do fluxo magnético^[10]. Associada a densidade de fluxo magnético está o campo magnético ${\displaystyle {\vec {H}}}$ que o gera, dado por ${\displaystyle H={\frac {B}{\mu }}}$. Perceba que com a redução da permeabilidade (na saturação), um maior campo magnético muito maior é demandado, e este, por fim, está associado à corrente elétrica ${\displaystyle I}$ que o gera, que por consequência, pode aumentar para valores muito acima dos nominais, mesmo com o transformador a vazio.

Para evitar este inconveniente deve-se trabalhar com valores baixos de saturação, limitando a tensão aplicada, aumentando a área de ferro ou aumentando a qualidade dos materiais.

Densidade de fluxo magnético ou Indução Magnética ${\displaystyle {\vec {B}}}$, cuja unidade é o tesla ${\displaystyle {\rm {T}}}$, ou webers por metro quadrado ${\displaystyle {\rm {Wb/m^{2}}}}$, é a medida da concentração do fluxo magnético ${\displaystyle \phi }$ ${\displaystyle \left({\rm {Wb}}\right)}$ em um devido material. Existem materiais que para um mesmo campo magnético ${\displaystyle {\vec {H}}}$ aplicado permitem diferentes passagens de densidade de fluxo magnético.

Motores, Geradores e Transformadores são feitos com materiais que permitem passar elevadas densidades de fluxo. Na região magneticamente linear a relação entre a densidade de fluxo e o campo magnético é dado por ${\displaystyle {\vec {B}}=\mu {\vec {H}}}$. Materiais ferromagnéticos facilmente tem permeabilidade magnética ${\displaystyle \mu }$ ${\displaystyle ({\rm {{H/m})}}}$ na ordem de mil a dez mil vezes^[1] a permeabilidade magnética do ar ${\displaystyle {{\mu }_{0}}=4\pi {{10}^{-7}}\,{\text{H/m}}}$.

Geração da Densidade de Fluxo Magnético

Geração de Campo Magnético a partir de Corrente Elétrica.

Imagine uma bobina enrolada no entorno de um material ferromagnético. A partir do momento que flui corrente no fio, um campo magnético ${\displaystyle \left(H={\frac {I}{2\pi r}}\right)}$///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 passa a circular ao redor deste (veja figura ao lado). Uma bobina é uma forma de se concentrar campo magnético. Uma vez aplicado o campo magnético ${\displaystyle {\vec {H}}}$ dá-se origem à indução magnética (ou densidade de fluxo magnético) ${\displaystyle {\vec {B}}=\mu {\vec {H}}}$. Associada a indução magnética está o fluxo magnético dado por ${\displaystyle \phi =\int \limits _{R}{{\vec {B}}\circ d{\vec {s}}}}$^[2][3] 

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle R}$ é a área que as linhas de fluxo atravessam.

A lei de Faraday-Neumann-Lenz^{[nota 1]}, ou lei da indução de Faraday, ou simplesmente, lei da indução eletromagnética, é uma das equações básicas do eletromagnetismo. Ela prevê como um campo magnético interage com um circuito elétrico para produzir uma força eletromotriz — um fenômeno chamado de indução eletromagnética. É a base do funcionamento de transformadores, alternadores, dínamos, indutores, e muitos tipos de motores elétricos, geradores e solenoides.^[1][2]

Atribui-se a Michael Faraday a descoberta da indução eletromagnética e, por conseguinte, o nome da lei relativa a esse fenômeno. Este foi comprovado experimentalmente por Faraday diversas vezes, apesar de sua explicação limitar-se ao conceito de linhas de força. A primeira formulação matemática da lei de Faraday foi feita por Franz Ernst Neumann em 1845. Nela, a força eletromotriz produzida em um circuito, pela indução, era expressa pelo negativo da derivada do fluxo magnético com o tempo através da área delimitada por esse circuito. O sinal negativo diz respeito ao sentido da FEM – e, por conseguinte, da corrente elétrica – e pode ser expressa formalmente por meio da chamada Lei de Lenz, desenvolvida por Heinrich Lenz em 1834, que integra o corolário da lei de Faraday.

Suas aplicações são inúmeras; na prática, quase todos os equipamentos eletro-eletrônicos utilizam o fenômeno da indução, seja para produzir uma corrente contínua, como nos dínamos, ou uma corrente alternada, como nos geradores, transformadores, alternadores e indutores, todos por meio da variação no campo magnético.

A equação de Maxwell–Faraday é uma generalização da lei de Faraday, e compõe uma das equações de Maxwell. Ela descreve como a variação de um campo magnético no tempo através de um circuito em repouso produz um campo elétrico não-eletrostático que, por sua vez, produz uma corrente elétrica no circuito. O movimento relativo entre um imã e o condutor e a produção, ou não, de um campo elétrico nessa experiência levaram a uma aparente dicotomia, exercendo, por sua vez, papel fundamental no desenvolvimento da relatividade restrita por Albert Einstein em 1905.

Índice

• 1História
• 2Lei de Faraday-Neumann-Lenz
  • 2.1Enunciado qualitativo
  • 2.2Enunciado quantitativo
  • 2.3Equação de Maxwell-Faraday
• 3Demonstração
• 4Contraexemplos
• 5A lei de Faraday e a relatividade
  • 5.1Dois fenômenos
  • 5.2Visões de Einstein
• 6Aplicações
  • 6.1Transformador
  • 6.2Gerador
• 7Notas
• 8Referências
• 9Ver também

História

A indução eletromagnética foi descoberta de forma independente por Michael Faraday em 1831 e Joseph Henry em 1832.^[3] Faraday, no entanto, foi o primeiro a publicar os resultados de seus experimentos.^[4] Em 29 de agosto de 1831, data da primeira demonstração experimental da indução eletromagnética feita por Faraday,^[5] ele amarrou dois fios em lados opostos de um anel de ferro (ou toro, um arranjo similar a um transformador toroidal moderno). Face às recém-descobertas propriedades do eletromagnetismo, ele esperava que, quando a corrente começasse a passar em um fio, uma espécie de onda viajaria através do anel e causaria algum efeito elétrico no lado oposto. Conectou, então, um dos fios a um galvanômetro e o outro a uma bateria. Foi observada, de fato, uma corrente transiente – que ele chamou de "onda de eletricidade" – nos momentos em que conectou e desconectou o fio à bateria.^[6] Esta indução ocorreu devido à mudança que houve no fluxo magnético quando a bateria foi conectada e desconectada.^[7]

Ilustração do aparato usado por Faraday em sua primeira demonstração da indução eletromagnética.

Faraday explicou a indução eletromagnética usando um conceito que chamou de linhas de força. No entanto, grande parte dos cientistas da época rejeitavam suas ideias teóricas, principalmente porque não havia uma formulação matemática para elas.^[8] James Clerk Maxwell, contudo, usou as ideias de Faraday como a base para sua teoria eletromagnética quantitativa.^[8][9] Nos estudos de Maxwell, o aspecto da variabilidade com o tempo da indução eletromagnética é expressado como uma equação diferencial, a qual Oliver Heaviside referiu-se como a lei de Faraday, embora seja diferente da versão original da lei de Faraday. A versão de Heaviside é a forma que hoje é reconhecida como parte do grupo de equações conhecido como equações de Maxwell.

A lei de Lenz, formulada por Heinrich Lenz em 1834, descreve o "fluxo através do circuito", e fornece a direção da força eletromotriz e corrente induzidas resultantes da indução eletromagnética.

Lei de Faraday-Neumann-Lenz

Enunciado qualitativo

A versão mais difundida da lei de Faraday afirma:

A força eletromotriz induzida em qualquer circuito fechado é igual ao negativo da variação do fluxo magnético com o tempo na área delimitada pelo circuito.^[10][11]

Esta versão da lei de Faraday é estritamente válida apenas quando o circuito fechado é um laço de fio metálico infinitamente fino,^[12] e é inválida em outras circunstâncias a serem discutidas. Uma versão diferente, a equação de Maxwell–Faraday, é válida em todas as circunstâncias.

Enunciado quantitativo

A lei da indução de Faraday faz uso do fluxo magnético Φ_B através de uma superfície hipotética Σ, cujo bordo é um laço de fio metálico. Uma vez que o laço pode estar se movendo com o tempo, escreve-se Σ(t) para a superfície. O fluxo magnético é definido pela integral de superfície:

${\displaystyle \Phi _{B}=\iint \limits _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,t)\cdot d\mathbf {A} \ }$,

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde dA é um elemento de área da superfície Σ(t), B é o campo magnético (também chamado de "densidade do fluxo magnético"), e B·dA é um produto escalar dos dois vetores (a quantidade infinitesimal de fluxo magnético). De outro modo, o fluxo magnético através do laço é proporcional ao número de linhas do fluxo magnético que passam por ele.

Quando o fluxo se modifica — devido a uma mudança do B, ou porque o laço é movido ou deformado, ou ambos — a lei da indução de Faraday afirma que o fio adquire uma FEM, ε, definida como o trabalho por unidade de carga que uma força não-eletrostática realiza quando uma carga é transportada em volta do laço.^{[12][13][14][nota 2]} De forma equivalente, é a voltagem que seria medida ao cortar o arame para criar um circuito aberto, ligando um voltímetro às pontas.

A lei de Faraday afirma que a FEM também é dada pela taxa de variação do fluxo magnético:

${\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt}\ }$,

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ε é a força eletromotriz (FEM) e Φ_B é o fluxo magnético. A direção da FEM é dada pela lei de Lenz.

Para um fio enrolado firmemente em uma bobina, composta de N voltas idênticas, cada uma com o mesmo Φ_B, a lei da indução de Faraday afirma:^[15][16]

${\displaystyle {\mathcal {E}}=-N{{d\Phi _{B}} \over dt}}$,

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde N é o número de voltas do fio e Φ_B é o fluxo magnético através de uma única volta.

Equação de Maxwell-Faraday

A equação de Maxwell-Faraday é uma generalização da lei de Faraday, e afirma que um campo magnético que varia com o tempo é sempre acompanhado por um campo elétrico não-conservativo que varia espacialmente, e vice-versa. A equação de Maxwell–Faraday é:

${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

(em unidades do SI), onde ${\displaystyle \nabla \times }$ é o operador rotacional e, novamente, E(r, t) é o campo elétrico e B(r, t) é o campo magnético. Tais campos podem estar em função da posição r e do tempo t.

A equação de Maxwell–Faraday é uma das quatro equações de Maxwell, tendo, portanto, um papel fundamental na teoria do eletromagnetismo clássico. Ela também pode ser escrita na forma integral pelo Teorema de Kelvin-Stokes:^[17]

${\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\iint _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {A} }$,///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde Σ é uma superfície limitada pelo seu bordo ∂Σ; E é o campo elétrico; B é o campo magnético; dℓ é um elemento vetorial infinitesimal de ∂Σ; dA é um elemento vetorial infinitesimal de Σ.

Ambos dℓ e dA têm uma ambiguidade de sinal; para obter o sinal correto, usa-se a regra da mão direita. Para uma superfície plana Σ, um elemento de curva positivo dℓ da curva ∂Σ é definido pela regra de mão direita como estando na direção dos dedos da mão direita quando o polegar aponta na direção do vetor normal n exterior à superfície Σ.

A lei de Gauss é a lei que estabelece a relação entre o fluxo do campo elétrico através de uma superfície fechada com a carga elétrica que existe dentro do volume limitado por esta superfície. A lei de Gauss é uma das quatro equações de Maxwell, juntamente com a lei de Gauss do magnetismo, a lei da indução de Faraday e a lei de Ampère-Maxwell. Foi elaborada por Carl Friedrich Gauss em 1835, porém só foi publicada após 1867.^[1] Gauss foi um matemático alemão que fez contribuições importantes para a teoria dos números, a geometria e a probabilidade, tendo também contribuições em astronomia e na medição do tamanho e do formato da Terra.^[2]

Índice

• 1Fluxo do campo elétrico
• 2Lei de Gauss
  • 2.1Forma integral da lei de Gauss
  • 2.2Forma diferencial da lei de Gauss
  • 2.3Relação entre a lei de Gauss e a lei de Coulomb
• 3Aplicações
  • 3.1Campo elétrico no interior e no exterior de uma esfera
  • 3.2Campo elétrico no interior e no exterior de uma casca esférica
  • 3.3Campo elétrico de um plano infinito
• 4Lei de Gauss para dielétricos
  • 4.1Cargas livres e cargas ligadas
  • 4.2Demonstração da lei de Gauss para dielétricos
• 5Referências
• 6Ver também

Fluxo do campo elétrico

Figura 1: Linhas de campo elétrico "furando" uma superfície, mostrando que o existe fluxo de campo elétrico através da superfície. Como as linhas de campo estão saindo da superfície, o fluxo do campo elétrico é positivo.

O fluxo de campo elétrico, ${\displaystyle \Phi _{E}}$, é uma grandeza escalar e pode ser considerado como uma medida do número de linhas de campo que atravessam a superfície.^[2][3] Convenciona-se que se há mais linhas de campo saindo da superfície do que entrando, o fluxo do campo elétrico através da superfície é positivo e se há mais linhas de campo entrando na superfície do que saindo da mesma, o fluxo é negativo. Além disso, é importante observar o fato de que se o número de linhas de campo que entra na superfície é igual ao número de linhas de campo que sai da superfície, então o fluxo de campo elétrico através da superfície é nulo,^[2][4] como pode ser visto na figura 2.

Para obter o fluxo do campo elétrico E através de uma superfície fechada em que E é não-uniforme, é preciso dividi-la em elementos de área infinitesimal dA. Define-se, então, um vetor dA cujo módulo é dA, a direção é perpendicular ao elemento de área e o sentido é adotado como o sentido da normal ao elemento infinitesimal saindo da superfície. Assim, esses elementos infinitesimais são tão pequenos que E pode ser considerado constante em todos os pontos de um mesmo elemento de área.^[2] Portanto, podemos definir o fluxo de E através de uma superfície S da seguinte forma:

${\displaystyle \Phi _{E}=\int _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

ou, no caso de uma superfície fechada:

${\displaystyle \Phi _{E}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} \,\!}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Da definição de produto escalar, tem-se que: E . dA = |E||dA| cosθ = |E|cosθ |dA|. Como θ é o ângulo entre os vetores E e dA, |E|cosθ é a projeção do vetor E sobre o vetor dA, logo a função desse produto escalar dentro da integral é selecionar algo proporcional à componente do campo elétrico que está "furando" à superfície infinitesimal dA, o que é coerente com a definição de fluxo dada anteriormente.

Por fim, se uma carga pontual estiver fora da superfície, as linhas de campo que partem da carga pontual irão entrar e sair da superfície, visto que as linhas de campo de uma carga pontual são radiais. Por isso, pode-se concluir que se uma carga está fora de uma superfície, então o fluxo do campo elétrico dessa carga através da superfície é nulo, ou seja:

${\displaystyle \Phi _{E}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =0}$, se ${\displaystyle q}$ estiver externa à superfície.

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Figura 2: As linhas de campo elétrico entram e saem da superfície, portanto o fluxo de campo elétrico sobre a superfície é nulo.

Lei de Gauss

A lei de Gauss estabelece uma relação entre o fluxo de campo elétrico através de uma superfície fechada e as cargas que estão no interior dessa superfície. Algumas considerações importantes sobre a de lei de Gauss são:

• A lei de Gauss não contém nenhuma informação que não esteja contida na lei de Coulomb e no princípio da superposição. Inclusive, é possível obter a lei de Coulomb a partir da lei de Gauss e vice-versa.^[3]
• É fundamental para a lei de Gauss, o fato de que a força elétrica é proporcional ao inverso do quadrado da distância. É esse fato que faz com que o fluxo de E não dependa da "superfície gaussiana" escolhida e dependa apenas das cargas que estão localizadas no interior da superfície. Dessa forma, é possível pensar numa lei de Gauss que estabeleça uma relação de fluxo para qualquer campo cuja lei de força associada a esse campo seja proporcional ao inverso do quadrado da distância, como a força gravitacional, por exemplo, logo existe uma lei de Gauss da gravitação.^[3]
• Apesar da lei de Coulomb nos fornecer o necessário para calcular o campo elétrico de uma distribuição de cargas, muitas vezes, as integrais que envolvem o cálculo do campo elétrico podem ser complicadas de serem resolvidas, mesmo para casos razoavelmente simples. É nesse ponto que reside um dos aspectos de maior eficiência da lei de Gauss: o cálculo do campo elétrico em distribuições de carga que possuam determinados tipos de simetria torna-se extremamente simples.^[3]
• A lei de Gauss se refere sempre ao fluxo no interior de uma superfície gaussiana escolhida. Portanto, para utilizar a lei de Gauss, é necessário definir o que é uma "superfície gaussiana". Esta é, por sua vez, uma superfície arbitrariamente escolhida. Normalmente, essa superfície é escolhida de modo que a simetria da distribuição de carga permita, ao menos em parte da superfície, um campo elétrico de intensidade constante.^[2]

Forma integral da lei de Gauss

Figura 3: Superfície gaussiana esférica centrada em q.

Para entender como a lei de Gauss relaciona o fluxo do campo elétrico no interior de uma superfície gaussiana com a carga no interior dessa mesma superfície, escolhe-se uma superfície qualquer com uma carga q em seu interior, como por exemplo a superfície da figura 1. Então, escolhe-se outra superfície gaussiana S' que está envolvendo q no interior de S. A forma dessa superfície S' pode ser qualquer, contudo, a fim de facilitar os cálculos e a visualização, vamos fazer dessa superfície S', uma esfera de raio r centrada na carga q, como por exemplo a superfície gaussiana representada na figura 3. O raio r é tal que S' esteja inteiramente dentro de S.^[4] O fluxo do campo elétrico através dessa esfera é dado por:

${\displaystyle \Phi _{E}=\oint _{S'}\mathbf {E} \cdot \mathrm {d} \mathbf {A} }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Como tanto E quanto dA são radiais, o produto escalar torna-se o produto dos módulos, então:

${\displaystyle \Phi _{E}=\oint _{S'}E\ dA}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Como |E| é constante na superfície da esfera, podemos tirá-lo da integral e temos:

${\displaystyle \Phi _{E}=E\oint _{S'}dA=\left({\frac {1}{4\pi \varepsilon _{0}}}{\frac {q}{r^{2}}}\right)(4\pi r^{2})={\frac {q}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Portanto, é possível observar que o fluxo através da superfície S' é um número que independe do raio da esfera. Dessa forma, o fluxo que sai da superfície S também será ${\displaystyle {\frac {q}{\varepsilon _{0}}}}$. Esse é um valor independente da forma da superfície S, desde que esta tenha uma carga q em seu interior. Se uma carga q está no exterior da superfície S, as suas linhas de campo entram e saem da superfície S, por isso, o fluxo de campo elétrico dessa carga sobre a superfície é nulo. Logo:

${\displaystyle \oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =0{\text{, se a carga está no exterior da superfície gaussiana.}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Por fim, se tivermos mais de uma carga no interior da superfície gaussiana, vale o princípio da superposição de modo que:

${\displaystyle \oint _{S}\left(\mathbf {E_{1}} +\mathbf {E_{2}} \right)\cdot \mathrm {d} \mathbf {A} =\oint _{S}\mathbf {E_{1}} \cdot \mathrm {d} \mathbf {A} +\oint _{S}\mathbf {E_{2}} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{1}+q_{2}}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Portanto, a Lei de Gauss na forma integral pode ser enunciada da seguinte forma:

${\displaystyle \oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Forma diferencial da lei de Gauss

[Expandir]Demonstração

Relação entre a lei de Gauss e a lei de Coulomb

[Expandir]Demonstração

Aplicações

É importante ressaltar que a lei de Gauss se torna eficiente apenas em casos em que há simetria. Mais precisamente, nos casos nos quais existe simetria esférica, cilíndrica ou plana.^[3] Dessa forma, construir superfícies gaussianas que aproveitem a simetria é de vital importância para a aplicação da lei de Gauss,^[2] visto que a eficiência da lei de Gauss consiste em utilizar a simetria das distribuições de carga para calcular campo elétrico dessas com mais facilidade.^[2][3]

Campo elétrico no interior e no exterior de uma esfera

Figura 4: Duas superfícies gaussianas esféricas em torno de uma esfera uniformemente carregada de raio R. A superfície gaussiana externa à esfera de raio R possui raio r' e a superfície gaussiana interna à esfera possui raio r.

Para uma esfera de raio R, como mostrada na figura 4, com carga Q uniformemente distribuída pela esfera, tem-se:

No exterior da esfera

Para se obter o campo no exterior da esfera, escolhe-se, como superfície gaussiana, a superfície esférica de raio r', situada no exterior da esfera de raio R, como mostra a figura 4. Pode-se imaginar que, muito longe da esfera, o campo elétrico que se sente é como o campo de uma carga puntiforme. Além disso, devido à simetria esférica, o campo elétrico deve apontar na direção radial. Dessa forma, aplicando a lei de Gauss:

${\displaystyle \oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}={\frac {Q}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O campo deve apontar na direção radial e, portanto, E e dA possuem a mesma direção e sentido e, por isso, segue que: E . dA = E dA. Logo:

${\displaystyle \oint _{S}E\ dA={\frac {Q}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O módulo do campo elétrico na superfície gaussiana é constante, visto que, nesse caso, o campo deve depender da distância em relação à esfera e, portanto, E pode sair da Integral.

${\displaystyle E\oint _{S}dA={\frac {Q}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E\left(4\pi r'^{2}\right)={\frac {Q}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r'^{2}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Logo:

${\displaystyle \mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r'^{2}}}{\hat {\mathbf {r} }}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

No interior da esfera

Para como o campo elétrico varia no interior da esfera, deve-se tomar como superfície Gaussiana a superfície esférica de raio r no interior da esfera de raio R, como mostra a figura 4. Nesse caso, como a carga está uniformemente distribuída pela esfera, a densidade volumétrica de carga, ρ, é a mesma em todos os pontos da esfera,então pode-se observar que:

${\displaystyle q_{int}=\rho V_{g}=\left({\frac {Q}{{\frac {4}{3}}\pi R^{3}}}\right)\left({\frac {4}{3}}\pi r^{3}\right)=Q\ {\frac {r^{3}}{R^{3}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde V_g é o volume da superfície gaussiana escolhida.

Dessa forma:

${\displaystyle \oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Os mesmos argumentos dados anteriormente para que o produto escalar E . dA seja E dA e para que E saia da integral continuam sendo válidos, logo:

${\displaystyle \oint _{S}E\ dA={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E\oint _{S}dA={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E\left(4\pi r^{2}\right)={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {r}{R^{3}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Logo:

${\displaystyle \mathbf {E} ={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {r}{R^{3}}}{\hat {\mathbf {r} }}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Portanto, no caso de uma esfera uniformemente carregada:

${\displaystyle \mathbf {E} ={\begin{cases}{\frac {Q}{4\pi \varepsilon _{0}}}{\frac {r}{R^{3}}}{\hat {\mathbf {r} }},&{\mbox{se }}r<R\\{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}}{\hat {\mathbf {r} }},&{\mbox{se }}r>R\end{cases}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Campo elétrico no interior e no exterior de uma casca esférica

Para se resolver esse problema, utiliza-se a figura 4 novamente, porém com uma ligeira diferença: o interior da esfera de raio R é "oco", isto é, tem-se apenas uma casca esférica com carga Q uniformemente distribuída sobre sua superfície.

No exterior da esfera

Escolhendo a superfície de raio r' como mostrada na figura 4, tem-se, pela lei de Gauss, o mesmo resultado que foi obtido para o campo no exterior de uma esfera. A carga interna à superfície gaussiana, q_int, é Q nesse caso, como no caso anterior da esfera uniformemente carregada, de forma que o cálculo para o campo elétrico exterior à da casca esférica se desenvolve da mesma forma que o cálculo para o campo no exterior à esfera uniformemente carregada, então:

${\displaystyle \mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r'^{2}}}{\hat {\mathbf {r} }}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

No interior da casca esférica

Escolhendo a superfície gaussiana de raio r, no interior da casca esférica, tem-se:

${\displaystyle \oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}=0}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle \oint _{S}E\ dA=0}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E\oint _{S}dA=0}$

${\displaystyle E\left(4\pi r^{2}\right)=0}$

Portanto:

${\displaystyle E=0}$

Logo:

${\displaystyle \mathbf {E} =\mathbf {0} }$

Portanto, no caso de uma casca esférica uniformemente carregada:

${\displaystyle \mathbf {E} ={\begin{cases}\mathbf {0} ,&{\mbox{se }}r<R\\{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}}{\hat {\mathbf {r} }},&{\mbox{se }}r>R\end{cases}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Campo elétrico de um plano infinito

Figura 5: Um exemplo de superfície gaussiana que se deve utilizar para obter o campo de um plano infinito é como a que está mostrada sobre a placa de baixo do capacitor.

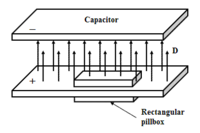
Supõe-se um plano infinito com densidade de carga σ e se deseja calcular o campo elétrico produzido por esse plano. Apesar de o problema ser bem diferente do apresentado na figura 5, visto que, no problema em questão, está-se estudando um plano infinito e não o campo no interior de um capacitor, é interessante utilizar uma superfície gaussiana de mesma forma que a superfície retratada na placa de baixo do capacitor da figura 5. Utilizando, portanto, a superfície de um paralelepípedo cortando o plano infinito como superfície S, tem-se:

${\displaystyle \oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Por simetria, o campo elétrico deve apontar para "fora" do plano, isto é, ele aponta na direção ${\displaystyle {\hat {\mathbf {z} }}}$ para pontos acima do plano e na direção ${\displaystyle -{\hat {\mathbf {z} }}}$ para pontos abaixo do plano. Dessa forma, as únicas superfícies superior e inferior da superfície do paralelepípedo é que serão "furadas" pelo campo elétrico, por isso:

${\displaystyle \oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =\int _{S1+S2}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =\int _{S1+S2}E\ dA=E\int _{S1+S2}dA=2AE}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde A é a área da superfície superior e inferior da superfície do paralelepípedo. Sabe-se, também, que : σ = qint/A, logo : qint = σA, portanto:

${\displaystyle 2AE={\frac {\sigma A}{\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E={\frac {\sigma }{2\varepsilon _{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

ou

${\displaystyle \mathbf {E} ={\frac {\sigma }{2\varepsilon _{0}}}{\hat {\mathbf {n} }}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle {\hat {\mathbf {n} }}}$ é um vetor unitário que aponta para fora da superfície do plano.

A lei de Coulomb é uma lei experimental^[1] da física que descreve a interação eletrostática entre partículas eletricamente carregadas. Foi formulada e publicada pela primeira vez em 1783 pelo físico francês Charles Augustin de Coulomb e foi essencial para o desenvolvimento do estudo da eletricidade.^[1]

Esta lei estabelece que o módulo da força entre duas cargas elétricas puntiformes (q₁ e q₂) é diretamente proporcional ao produto dos valores absolutos (módulos) das duas cargas e inversamente proporcional ao quadrado da distância r entre eles. Esta força pode ser atrativa ou repulsiva dependendo do sinal das cargas. É atrativa se as cargas tiverem sinais opostos. É repulsiva se as cargas tiverem o mesmo sinal.

Sendo uma lei do inverso do quadrado , a lei é análoga à lei do inverso do quadrado da gravitação universal de Isaac Newton , mas as forças gravitacionais são sempre atrativas, enquanto as forças eletrostáticas podem ser atrativas ou repulsivas.^[2] A lei de Coulomb pode ser usada para derivar a lei de Gauss e vice-versa. No caso de uma única carga pontual estacionária, as duas leis são equivalentes, expressando a mesma lei física de maneiras diferentes.^[3] A lei foi testada extensivamente e as observações confirmaram a lei na escala de 10 ⁻¹⁶ m á 10 ⁸ m.^[4]

Índice

• 1História
• 2Definição
  • 2.1Forma escalar da lei
  • 2.2Forma vetorial da lei
  • 2.3Constante de Coulomb
  • 2.4Limitações
• 3Campos elétricos
• 4Experimento simples para verificar a lei de Coulomb
• 5Notas
• 6Referências

História

Os primeiros investigadores do século 18 que suspeitaram que a força elétrica diminuía com a distância como a força da gravidade (ou seja, como o inverso do quadrado da distância) incluíram Daniel Bernoulli^[5] e Alessandro Volta , ambos medindo a força entre as placas de um capacitor e Franz Aepinus que supôs a lei do inverso do quadrado em 1758.^[6]

Com base em experimentos com esferas eletricamente carregadas, Joseph Priestley, em 1767, foi um dos primeiros a propor que a força elétrica seguia uma lei do inverso do quadrado, semelhante à lei da gravitação universal de Newton.^[7] No entanto, ele não generalizou ou elaborou sobre isso.^[8] Em 1767, ele conjeturou que a força entre as cargas variava como o inverso do quadrado da distância.^[9][10]

Em 1769, o físico escocês John Robison anunciou que, de acordo com suas medições, a força de repulsão entre duas esferas com cargas do mesmo sinal variava em x ^-2,06 .^[11]

No início da década de 1770, a dependência da força entre corpos carregados em relação à distância e à carga já havia sido descoberta, mas não publicada, por Henry Cavendish da Inglaterra.^[12]

Charles Augustin Coulomb foi o primeiro a realizar uma investigação experimental direta da lei de forças.^[13] Em 1785, ele publicou três relatórios sobre eletricidade e magnetismo, onde declarou o que veio a ser conhecido como Lei de Coulomb. Ele utilizou uma balança de torção para estudar as forças de repulsão e atração de partículas carregadas e determinou que a magnitude da força elétrica entre duas cargas pontuais é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas.

A balança de torção consiste em uma barra suspensa em seu meio por uma fibra fina. A fibra atua como uma mola de torção muito fraca. No experimento de Coulomb, a balança de torção era uma haste isolante com uma bola revestida de metal presa a uma extremidade, suspensa por um fio de seda. A bola foi carregada com uma carga conhecida de eletricidade estática, e uma segunda bola carregada da mesma polaridade foi trazida para perto dela. As duas bolas carregadas se repeliam, torcendo a fibra em um determinado ângulo, que podia ser lido em uma escala do instrumento. Ao saber quanta força era necessária para torcer a fibra através de um determinado ângulo, Coulomb foi capaz de calcular a força entre as bolas e deduzir a lei da proporcionalidade do inverso do quadrado.

Definição

Balança de Coulomb

A lei de Coulomb afirma que:

A magnitude das forças eletrostáticas com as quais duas cargas pontuais em repouso interagem é diretamente proporcional ao produto da magnitude de ambas as cargas e inversamente proporcional ao quadrado da distância que as separa.^{[nota 1]}

A força eletrostática atua ao longo da linha reta entre as cargas. Se ambas as cargas possuem o mesmo sinal, a força eletrostática entre elas será de repulsão; se elas possuírem sinais diferentes, a força entre elas será de atração.

A lei de Coulomb também pode ser expressa como uma expressão matemática simples. As formas escalar e vetorial da equação matemática são:

Forma escalar da lei

A forma escalar fornece a magnitude do vetor da força eletrostática ${\displaystyle F}$ entre duas cargas pontuais q₁ e q₂ mas não sua direção. Se ${\displaystyle r}$ é a distância entre as cargas, a magnitude da força é

${\displaystyle |\mathbf {F} |=k_{\text{e}}{|q_{1}q_{2}| \over r^{2}}\qquad }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde:

• ${\displaystyle k_{e}}$ é a Constante de Coulomb (${\displaystyle k_{e}}$ = 8.9875517873681764×10⁹ N⋅m²⋅C⁻² );
• ${\displaystyle q_{1}}$ e ${\displaystyle q_{2}}$ são as magnitudes sinalizadas das cargas, expressas em Coulomb (C)
• a força eletrostática é dada em Newtons (N )

Forma vetorial da lei

A lei de Coulomb afirma que a força eletrostática ${\displaystyle F}$₁ experimentado por uma carga, q₁ na posição ${\displaystyle r}$₁ nas proximidades de outra carga, q₂ na posição ${\displaystyle r}$₂ no vácuo é igual a:

Diagrama que descreve o mecanismo básico da lei de Coulomb. As cargas iguais se repelem e as cargas opostas se atraem

${\displaystyle \qquad \mathbf {F} _{1}=k_{\text{e}}{\frac {q_{1}q_{2}}{{|\mathbf {r} _{12}|}^{2}}}\mathbf {\widehat {r}} _{12},\qquad }$///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde:

• o escalar ${\displaystyle r}$ é a distância entre as cargas, dada em metros (m)

• ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

• o vetor ${\textstyle r_{12}=r_{1}-r_{2}}$ é a distância vetorial entre as cargas, e ${\textstyle {\widehat {\mathbf {r} }}_{12}={\frac {\mathbf {r_{12}} }{\mathbf {|r_{12}|} }}}$ ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  (um vetor de unidade apontando de ${\textstyle q_{2}}$ a ${\textstyle q_{1}}$).
• a força eletrostática é dada em Newtons (N)

A forma vetorial da lei de Coulomb é simplesmente a definição escalar da lei com a direção dada pelo vetor unitário, ${\displaystyle {\hat {r}}}$₁₂, paralelo com a linha de carga q₂ a carga q₁.^[14] Se ambas as cargas tiverem o mesmo sinal (como cargas), o produto q₁q₂ é positivo e a direção da força sobre q₁ é dado por ${\displaystyle {\hat {r}}}$₁₂ as cargas repelem. Se as cargas tiverem sinais opostos, o produto q₁q₂ é negativo e a direção da força sobre q₁ é -${\displaystyle {\hat {r}}}$₁₂ as cargas se atraem.

A força eletrostática ${\displaystyle F}$2 experimentado por q₂, de acordo com a terceira lei de Newton , é ${\displaystyle F}$2 = ${\displaystyle -F}$1.///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

No sistema CGS de unidades, que adota cm, g, s como unidades básicas, toma-se ${\displaystyle k=1}$ para interação entre cargas no vácuo, e define-se a unidade de carga como aquela que exerce uma força de 1 dina sobre outra carga idêntica à distância de 1 cm.^[13]

Constante de Coulomb

Ver artigo principal: Constante de Coulomb

A constante de Coulomb é um fator de proporcionalidade que aparece na lei de Coulomb, bem como em outras fórmulas relacionadas à eletricidade. O valor dessa constante depende do meio em que os objetos carregados estão imersos. Denotada, também é chamada de constante de força elétrica ou constante eletrostática,^[15] daí o subscrito ${\displaystyle e}$.

Antes da redefinição das unidades do SI, a constante de Coulomb no vácuo era considerada como tendo um valor exato:

${\displaystyle {\begin{aligned}k_{\text{e}}&={\frac {1}{4\pi \varepsilon _{0}}}={\frac {c_{0}^{2}\mu _{0}}{4\pi }}=c_{0}^{2}\times 10^{-7}\ {H\cdot m}^{-1}\\&=8.987\,551\,787\,368\,176\,4\times 10^{9}\ {N\cdot m^{2}\cdot C}^{-2}.\end{aligned}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Desde a redefinição,^[16][17] a constante de Coulomb não é mais exatamente definida e está sujeita ao erro de medição. Conforme calculado a partir dos valores recomendados do CODATA 2018, a constante de Coulomb é^[18]

${\displaystyle k_{\text{e}}=8.987\,551\,792\,3\,(14)\times 10^{9}\ {N\cdot m^{2}\cdot C}^{-2}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em unidades Gaussianas e unidades Lorentz-Heaviside , que são ambos sistemas de unidades CGS , a constante tem diferentes valores adimensionais .

Em unidades electrostáticas ou unidades gaussianas a unidade de carga ( ESU ou statcoulomb ) é definida de tal modo que a constante de Coulomb desaparece, uma vez que tem o valor de um e torna-se adimensional.

${\displaystyle k_{\text{e}}=1}$ (Unidades gaussianas).

Em unidades de Lorentz-Heaviside, também chamadas de unidades racionalizadas , a constante de Coulomb é adimensional e é igual a:

${\displaystyle k_{\text{e}}={\frac {1}{4\pi }}}$ 

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

(Unidades Lorentz-Heaviside)

As unidades gaussianas são mais adequadas para problemas microscópicos, como a eletrodinâmica de partículas individuais eletricamente carregadas.^[19] As unidades SI são mais convenientes para fenômenos práticos de grande escala, como aplicações de engenharia.^[20]