sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O paramagnetismo consiste na tendência que os dipolos magnéticos atômicos têm de se alinharem paralelamente com um campo magnético externo. Este efeito ocorre devido ao spin mecânico-quântico, assim como o momento angular orbital dos elétrons. Caso estes dipolos magnéticos estejam fortemente unidos então o fenômeno poderá ser o ferromagnetismo ou o ferrimagnetismo.

Este alinhamento dos dipolos magnéticos atômicos tende a se fortalecer e é descrito por uma permeabilidade magnética relativa maior do que a sua unidade (ou, equivalentemente, uma susceptibilidade magnética positiva e pequena).

O paramagnetismo requer que os átomos possuam, individualmente, dipolos magnéticos permanentes, mesmo sem um campo aplicado, o que geralmente implica um átomo desemparelhado com os orbitais atômicos ou moleculares.

No paramagnetismo puro, estes dipolos atômicos não interagem uns com os outros e são orientados aleatoriamente na ausência de um campo externo, tendo como resultado um momento líquido zero. No caso de existir uma interação, então podem espontaneamente se alinhar ou antialinhar-se, tendo como resultado o ferromagnetismo ou o antiferromagnetismo, respectivamente. O comportamento paramagnético pode também ser observado nos materiais ferromagnéticos que estão acima da temperatura de Curie, e nos antiferromagnéticos acima da temperatura de Néel.

Em átomos sem dipolo magnético, um momento magnético pode ser induzido em uma direção anti-pararela a um campo aplicado, este efeito é chamado de diamagnetismo. Os materiais paramagnéticos podem também exibir o diamagnetismo, mas tipicamente com valores fracos.

Os materiais paramagnéticos em campos magnéticos sofrem o mesmo tipo de atração e repulsão que os ímãs normais, mas quando o campo é removido o movimento Browniano rompe o alinhamento magnético. No geral os efeitos paramagnéticos são pequenos (susceptibilidade magnética na ordem entre 10-3 e 10-5).

Índice

• 1Lei de Curie
• 2Materiais paramagnéticos
• 3Ilustrações de prova do paramagnetismo
• 4Ver também
• 5Referências
• 6Ligações externas

Lei de Curie

Sob baixos campos magnéticos, os materiais paramagnéticos exibem a magnetização na mesma direção do campo externo, e de acordo com a lei de Curie:

${\displaystyle \mathbf {M_{R}} =C\cdot {\frac {\mathbf {B} }{T}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde:

M_R é a magnetização resultante;

B é a densidade do fluxo magnético do campo aplicado, medido em tesla;

T é a temperatura absoluta, medida em kelvin;

C é uma constante específica de cada material (sua Constante de Curie).

Esta lei indica que os materiais paramagnéticos tendem a se tornar cada vez mais magnéticos enquanto o campo magnético aumentar, e cada vez menos magnéticos ao aumentar a temperatura. A lei de Curie é incompleta, pois não prediz a saturação que ocorre quando a maioria dos dipolos magnéticos estão alinhados, pois a magnetização será a máxima possível, e não crescerá mais, independentemente de aumentar o campo magnético ou diminuir-se a temperatura.

Materiais paramagnéticos

• Sódio Na [11] (metal alcalino)
• Magnésio Mg [12] (metal alcalino-terroso)
• Cálcio Ca [20] (metal alcalino-terroso)
• Estrôncio Sr [38] (metal alcalino-terroso)
• Bário Ba [56] (metal alcalino-terroso)
• Alumínio Al [13] (metal terroso) É o material paramagnético preferido para aplicações em catapultas eletromagnéticas lunares, utilizando rególito como minério.
• Oxigênio O [8] (ametal calcogênio) Na forma líquida.
• Tecnécio Tc [43] (metal de transição externa) (elemento artificial)
• Platina Pt [78] (metal de transição externa) (metal nobre)
• Urânio U [92] (metal de transição interna) (actinídeo)
• Óxido Nítrico NO [15] (composto gasoso da categoria dos monóxidos)

Ilustrações de prova do paramagnetismo

Pequenos imãs na ausência de um campo magnético

Pequenos imãs sob um campo magnético fraco

Pequenos imãs sob um campo magnético forte

Diamagnetismo é o termo utilizado para designar o comportamento de materiais que são repelidos na presença de campos magnéticos, ao contrário dos materiais paramagnéticos e ferromagnéticos que são atraídos por campos magnéticos.

Uma levitação diamagnética.

O diamagnetismo é um efeito quântico que existe em todos os materiais, mas é tão fraco que normalmente não pode ser observado quando o material possui uma das outras duas propriedades: ferromagnetismo ou paramagnetismo.^[1] Ou seja, o diamagnetismo corresponde ao tipo mais fraco de resposta magnética de um sistema.^[2]

Nos materiais diamagnéticos, os dipolos elementares não são permanentes, sendo que esses materiais não são afetados com a mudança de temperatura e o valor da sua susceptibilidade magnética é tipicamente próximo de milionésimo (10⁻⁶) e sempre negativo, devido a Lei de Lenz que afirma que um circuito submetido a um campo magnético externo variável, cria um campo contrário opondo-se a variação deste campo externo.^[2] Devido ao valor da susceptibilidade magnética ser negativo, o material sofre uma repulsão, entretanto o efeito é muito fraco, isto é, somente é percebido em campos magnéticos intensos, algumas ordens de grandeza maior do que o campo magnético terrestre.

Todo material diamagnético submetido a um campo magnético externo apresenta um momento dipolar magnético líquido orientado no sentido oposto ao do campo magnético externo. Se o campo magnético externo é não-uniforme, o material diamagnético é repelido da região onde o campo magnético é mais intenso para a região onde o campo magnético é menos intenso.^[1]

Índice

• 1História
• 2Materiais
  • 2.1Supercondutividade
• 3Teoria
  • 3.1Diamagnetismo de Langevin
• 4Demonstrações
  • 4.1Curvando a superfície da água
  • 4.2Levitação
• 5Ver também
• 6Referências
• 7Ligações externas

História

Foi primeiramente observado por Sebald Justinus Brugmans em 1778, ao observar que o bismuto e o antimônio eram repelidos por campos magnéticos. O diamagnetismo foi nominado e estudado por Michael Faraday, em 1845 que, através de seus estudos, concluiu que o diamagnetismo era uma propriedade da matéria, e que todo material respondia de uma forma diamagnética ou de uma forma paramagnética a um campo magnético aplicado a ele.^[3]

Materiais

Materiais diamagnéticos como a água, ou materiais que tenham a água como base, tem uma permeabilidade magnética relativa menor ou igual a 1, consequentemente sua susceptibilidade magnética é menor ou igual a zero, já que a susceptibilidade é definida por χ_v = μ_v − 1. Isso indica que materiais diamagnéticos são repelidos por campos magnéticos. Contudo, como o diamagnetismo é uma propriedade fraca, seus efeitos não podem ser observados no dia a dia. Por exemplo, a susceptibilidade magnética de diamagnéticos como a água é da ordem de χ_v = −9,05×10⁻⁶. O material diamagnético mais forte é o bismuto, χ_v = −1,66×10⁻⁴, mesmo que o grafite pirolítico possa ter susceptibilidade de χ_v = −4,00×10⁻⁴ em um dos planos. Mesmo assim, estes valores são de ordem de magnitude muito inferior ao magnetismo que possuem os materiais paramagnéticos e ferromagnéticos.

Todos os condutores mostram um diamagnetismo mais efetivo quando interagem com um campo magnético que varia no tempo. A força de Lorentz que age nos elétrons faz com que eles se movimentem formando correntes parasitas, que por sua vez produzem um campo magnético induzido no sentido oposto ao campo aplicado.

Supercondutividade

Transição da condutividade normal (esquerda) para a supercondutividade (direita). Durante a transição, o condutor repele o campo magnético e age como um diamagnético perfeito.

Supercondutores são materiais que perdem a resistência à corrente elétrica quando estão abaixo de uma determinada temperatura. O supercondutor é um diamagnético perfeito (χ_v = −1). pois ele repele todos os campos magnéticos (exceto em superfícies muito finas) devido ao Efeito Meissner. Esse efeito, que talvez seja a característica mais famosa dos supercondutores, é a causa da levitação magnética de um ímã, por exemplo, quando é colocado sobre um pedaço de supercondutor. A explicação para o fenômeno está na repulsão total dos campos magnéticos externos pelos supercondutores, o que faz com que o campo magnético interno seja nulo, desde que o campo externo aplicado não seja muito intenso.^[4]

Principais materiais diamagnéticos^[5] (O valor da susceptibilidade χ_v é adimensional)

Material	χv [x 10−5]
Supercondutor	-105
Grafite Pirolítico	-40,9
Bismuto	-16,6
Mercúrio	-2,9
Prata	-2,6
Diamante	-2,1
Chumbo	-1,8
Grafite	-1,6
Cobre	-1,0
Água	-0,91

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Teoria

Em um material, normalmente os elétrons se dispõe em órbitas, sem nenhuma resistência entre elas agindo como um loop de corrente. Deste modo, poderia se dizer que em geral os efeitos do diamagnetismo seriam comuns, visto que qualquer campo magnético aplicado gerariam corrente nesses loops em oposição à carga, de um modo similar aos supercondutores, que essencialmente são diamagnéticos perfeitos. Entretanto, como os elétrons são mantidos presos às órbitas pela carga dos prótons e ainda mais pelo Princípio de Exclusão de Pauli, muitos materiais exibem o diamagnetismo mas respondem muito pouco aos campos magnéticos aplicados.

O Teorema de Bohr-Van Leewen^[6][7] prova que não pode haver paramagnetismo ou diamagnetismo em um sistema puramente clássico, Porém, a teoria clássica de Paul Langevin para o diamagnetismo nos dá a mesma previsão que a teoria quântica. A teoria clássica é dada abaixo:

Diamagnetismo de Langevin

A teoria do diamagnetismo de Langevin^[8] se aplica a materiais que contém átomos O número de revoluções por unidade de tempo é com "cascas fechadas" (ver dielétrico). Um campo magnético com intensidade B, aplicado a um elétron com carga e e massa m, dá início à precessão de Larmor com uma frequência ω = eB / 2m. O número de revoluções por unidade de tempo é ω / 2π. Então a corrente elétrica para um átomo com Z elétrons é (em unidades do SI):

${\displaystyle I=-{Ze^{2}B \over 4\pi m}}$. ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O momento magnético de um loop de corrente é igual a corrente vezes a área do loop. Suponha que o campo é alinhado com o eixo z, a área média do loop pode ser dada por π(ρ²) , onde (ρ²) é a raíz quadrada da distância dos elétrons perpendiculares ao eixo z. O momento magnético é, portante:

${\displaystyle \mu =-{Ze^{2}B \over 4m}(\rho ^{2})}$. ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Se a distribuição da carga é esfericamente simétrica, podemos supor que a distribuição das coordenadas x, y, z são independentes e igualmente distribuídas. Então ${\displaystyle \langle x^{2}\rangle =\langle y^{2}\rangle =\langle z^{2}\rangle ={1 \over 3}\langle r^{2}\rangle }$. ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 Onde. ${\displaystyle \langle r^{2}\rangle }$é a raiz quadrada da distância dos elétrons até o núcleo, portanto ${\displaystyle \langle \rho ^{2}\rangle =\langle x^{2}\rangle +\langle y^{2}\rangle ={2 \over 3}\langle r^{2}\rangle }$. S ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

e n é o número de átomos por unidade de volume, a susceptibilidade magnética do volume é, em unidades do SI:

${\displaystyle \mathrm {X} ={\mu _{0}n\mu \over B}=-{\mu _{0}e^{2}Zn \over 6m}\langle r^{2}\rangle }$ ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ferromagnetismo é o mecanismo básico pelo qual certos materiais (como ferro) formam ímãs permanentes, ou são atraídos por ímãs. Na física, vários tipos diferentes de magnetismo são distinguidos. Ferromagnetismo (incluindo ferrimagnetismo) é o tipo mais forte e é responsável por fenômenos comuns do magnetismo encontradas na vida cotidiana. Outras substâncias respondem fracamente a campos magnéticos com dois outros tipos de magnetismo o paramagnetismo, e o diamagnetismo, mas as forças são tão fracas que elas só podem ser detectadas por instrumentos sensíveis em um laboratório. Um exemplo corriqueiro de ferromagnetismo é um ímã de geladeira usado para guardar notas em uma porta do refrigerador.

Um material ferromagnético tem um momento magnético espontâneo – um momento magnético mesmo em um campo magnético aplicado igual a zero. A existência de um momento espontâneo sugere que os spins dos elétrons e os seus momentos magnéticos estão arranjados de uma maneira regular. O ferromagnetismo é encontrado em ligas binárias e ternárias de ferro, níquel, cobalto com outros elementos,^[1] alguns compostos de metais de terras raras, e alguns minerais de ocorrência natural, tais como magnetita.

Índice

• 1História e distinção do ferrimagnetismo
• 2Ciclo de histerese
  • 2.1Origem física
    • 2.1.1Aplicações
• 3Método de medição dos campos
• 4Temperatura de Curie
• 5Modelos teóricos
  • 5.1Hamiltoniana de Heisenberg
  • 5.2Modelo de Weiss
• 6Materiais ferromagnéticos
• 7Ver também
• 8Referências
• 9Bibliografia

História e distinção do ferrimagnetismo

Historicamente, o termo ferromagnético foi usado para qualquer material que exibisse magnetização espontânea, i.e, um momento magnético na ausência de um campo magnético externo. Esta definição geral é ainda de uso comum. Mais recentemente, no entanto, diferentes classes de magnetização espontânea foram identificadas. Em particular, um material é ferromagnético somente se todos os seus íons magnéticos adicionarem uma contribuição positiva para a magnetização líquida. Se alguns dos íons magnéticos subtrair a magnetização líquida (se forem parcialmente antialinhados), então o material é ferrimagnético. Se os momentos dos íons alinhados e antialinhados forem iguais, de modo a ter magnetização líquida zero, apesar do ordenamento magnético, então o material é um antiferromagneto. Estes efeitos de alinhamento só ocorrem em temperaturas abaixo de uma determinada temperatura crítica, denominada temperatura Curie (para ferromagnetos e ferrimagnetos) ou a temperatura Néel (para antiferromagneto).

Ciclo de histerese

Quando um campo magnético externo é aplicado a um ferromagneto como o ferro, os dipolos atômicos irão alinhar-se com ele. Mesmo quando o campo é removido, parte do alinhamento vai ser mantido: o material tornou-se magnetizado. Uma vez magnetizado, o imã vai ficar magnetizado por tempo indeterminado. Para desmagnetizar exige-se aplicação de calor ou de um campo magnético na direção oposta. Este é o efeito que fornece o elemento de memória em uma unidade de disco rígido.

A relação entre a indução magnética H e a magnetização M não é linear em tais materiais. Se um ímã é desmagnetizado (H = M = 0) e a relação entre H e M é plotada para aumento dos níveis de intensidade de campo, M segue a curva de magnetização inicial. Esta curva aumenta rapidamente no início e depois se aproxima de uma assíntota chamada saturação magnética. Se o campo magnético é agora reduzido monotonicamente, M segue uma curva diferente. Em uma intensidade de campo igual a zero, a magnetização é compensada a partir da origem de um montante chamado de remanência. Se a relação entre H e M for traçado para todas as forças de campo magnético aplicado o resultado é um ciclo de histerese chamado de loop principal.

Um olhar mais atento em uma curva de magnetização geralmente revela uma série de pequenos saltos aleatórios na magnetização chamados saltos Barkhausen. Este efeito é devido a defeitos cristalográficos tais como deslocamentos.

Origem física

O fenômeno da histerese em materiais ferromagnéticos é o resultado de dois efeitos: a rotação do vetor magnetização e as mudanças no tamanho ou número de domínios magnéticos. Em geral, a magnetização varia (em direção, mas não magnitude) através de um ímã.

Ímãs maiores são divididos em regiões chamadas de domínios. Em cada domínio, a magnetização não varia, mas entre os domínios temos paredes de domínio relativamente finas em que a direção da magnetização gira na direção de um domínio para outro. Se o campo magnético muda, as paredes se movem, mudando assim o tamanho relativo dos domínios.

Aplicações

Há uma grande variedade de aplicações da histerese em ferromagnetos. Muitos destes fazem uso de sua capacidade de reter memória, por exemplo, cartões de fita magnética, discos rígidos, e de crédito. Nestas aplicações, ímãs de disco rígido como o ferro são desejáveis para a memória não ser facilmente apagada.

Método de medição dos campos

O método descrito pelo ciclo de histerese mede o campo de indução magnética ${\displaystyle \mathbf {B} }$ em função do campo magnético ${\displaystyle \mathbf {H} }$. Se considerarmos um anel de material ferromagnético de seção A e raio R constante, envolvido por N espiras pelas quais passa uma corrente contínua I. Nesta situação, os campos são circulares dentro do anel e são desprezíveis fora dele. Deste modo se calcula o valor de ${\displaystyle \mathbf {H} }$ a partir da Lei de Ampère:

${\displaystyle \oint _{C}\mathbf {H} \cdot d\mathbf {l} =N\ I}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

e, como o anel tem simetria circular, a integral resulta:

${\displaystyle H\cdot 2\pi R=N\ I\Longrightarrow H={\frac {N\ I}{2\pi R}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Levando em conta a permeabilidade magnética relativa do material ${\displaystyle \mu _{r}}$, é possível calcular o campo de indução magnética:

${\displaystyle B=\mu _{0}\mu _{r}\ H=\mu \ H}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Este sistema é usado na prática para medir os dois campos ao variar a intensidade da corrente:

${\displaystyle H\cdot 2\pi R=N\ I}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Uma vez medidos ${\displaystyle \mathbf {H} }$ e ${\displaystyle \mathbf {B} }$ se pode encontrar o valor da magnetização ${\displaystyle \mathbf {M} }$:

${\displaystyle \mathbf {H} ={\frac {\mathbf {B} -\mu _{0}\mathbf {M} }{\mu _{0}}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Por meio desse procedimento é possível obter experimentalmente a curva de magnetização, ou a variação do campo magnético em função do vetor de indução magnética e, portanto, o ciclo de histerese.

Temperatura de Curie

Marie Curie foi a primeira a descobrir que existe uma temperatura crítica para cada material ferromagnético acima da qual o material se comporta como paramagnético. Quando a temperatura aumenta, o movimento térmico compete com a tendência ferromagnética para os dipolos se alinharem. Quando a temperatura sobe além de certo ponto, chamado de temperatura Curie, há uma transição de fase de segunda ordem e o sistema não pode mais manter uma magnetização espontânea, embora ainda responda paramagneticamente a um campo externo. Abaixo dessa temperatura, há uma quebra espontânea de simetria e forma-se domínios aleatórios (na ausência de um campo externo). A Susceptibilidade magnética segue a lei de Curie-Weiss:

${\displaystyle \chi _{m}={\frac {C\ \rho }{T-T_{c}}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde C é uma constante característica do material, ${\displaystyle \rho }$ sua densidade e ${\displaystyle T_{c}}$ a temperatura de Curie em kelvin.

Modelos teóricos

O ferromagnetismo representa um dos principais problemas em aberto da física do estado sólido. Existem dois modelos teóricos que o descrevam: o modelo de Ising e o modelo de Weiss, o qual será tratado a seguir, ambos sendo baseados na hamiltoniana de Werner Karl Heisenberg, mas que utilizam grandes aproximações.

Hamiltoniana de Heisenberg

A hamiltoniana para um par de elétrons pertencentes a átomos vizinhos é:

${\displaystyle H=H_{1}+H_{2}+V_{12}\ }$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle H_{1}}$ e ${\displaystyle H_{2}}$  ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

são as hamiltonianas apenas dos elétrons, e ${\displaystyle V_{12}}$ é a interação entre os dois.

Pelo princípio de exclusão de Pauli, a função de onda total deve ser antissimétrica. Assim, tem-se duas possibilidades:

${\displaystyle \varphi _{A}=\psi _{S}(\mathbf {r} _{1},\mathbf {r} _{2})\chi _{A}(\mathbf {\sigma } _{1},\mathbf {\sigma } _{2})}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

ou

${\displaystyle \varphi _{A}=\psi _{A}(\mathbf {r} _{1},\mathbf {r} _{2})\chi _{S}(\mathbf {\sigma } _{1},\mathbf {\sigma } _{2})}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde os subscritos “A” ou “S” indicam uma função antissimétrica/simétrica.

As funções de onda de spin para um par de elétrons são:

${\displaystyle \chi _{S}:\left\{{\begin{matrix}|++\rangle \qquad [\mathbf {s} _{z}=1]\\{\frac {1}{\sqrt {2}}}(|+-\rangle +|-+\rangle )\quad [\mathbf {s} _{z}=0]\\|--\rangle \qquad [\mathbf {s} _{z}=-1]\\\end{matrix}}\right.}$

${\displaystyle \chi _{A}:{\frac {1}{\sqrt {2}}}(|+-\rangle -|-+\rangle )\quad [\mathbf {s} _{z}=0]}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

As funções de onda “espaciais” são:

${\displaystyle \psi _{S}:{\frac {1}{\sqrt {2}}}(\psi _{1}(\mathbf {r} _{1})\psi _{2}(\mathbf {r} _{2})+\psi _{1}(\mathbf {r} _{2})\psi _{2}(\mathbf {r} _{1}))}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle \psi _{A}:{\frac {1}{\sqrt {2}}}(\psi _{1}(\mathbf {r} _{1})\psi _{2}(\mathbf {r} _{2})-\psi _{1}(\mathbf {r} _{2})\psi _{2}(\mathbf {r} _{1}))}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Efetuando um cálculo perturbativo sobre tais funções de onda obtêm-se:

${\displaystyle E=\left\{{\begin{matrix}E_{0}+J\quad \rightarrow \quad \varphi _{1}=\psi _{S}\chi _{A}\\E_{0}-J\quad \rightarrow \quad \varphi _{2}=\psi _{A}\chi _{S}\\\end{matrix}}\right.}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde J é conhecida como integral de troca, que está relacionada com a Interação de Troca, interação responsável pela tendência dos momentos magnéticos do material a permanecerem paralelos entre si. A hamiltoniana separa, então, os estados com spins diferentes, e por este motivo, Heisenberg encontrou um operador que distinguisse os estados com spin diferente e que então pudesse descrever a interação precedente. Tal operador é:

${\displaystyle \mathbf {s} _{1}\cdot \mathbf {s} _{2}=\left\{{\begin{matrix}-{\frac {3}{4}}\quad \rightarrow \varphi _{1}\\{\frac {1}{4}}\quad \rightarrow \varphi _{2}\\\end{matrix}}\right.}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Logo, a Hamiltoniana de Heisenberg é:

${\displaystyle H_{Heisenberg}=-2J\mathbf {s} _{1}\cdot \mathbf {s} _{2}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Modelo de Weiss

O modelo de Weiss propõe a generalização da hamiltoniana de Heisenberg para um sistema com mais elétrons, utilizando uma aproximação de campo médio: um elétron sofre uma interação devida à média do campo gerado pelos outros elétrons.

A Hamiltoniana do sistema torna-se então:

${\displaystyle H_{magn}=g_{0}\mu _{B}\mathbf {s} (\mathbf {r} )\cdot \mathbf {B} -\sum _{\mathbf {r} '}J(\mathbf {r} -\mathbf {r} ')\mathbf {s} (\mathbf {r} )\mathbf {s} (\mathbf {r} ')=s(\mathbf {r} )\cdot \langle g_{0}\mu _{B}\mathbf {B} -\sum _{\mathbf {r} '}J(\mathbf {r} -\mathbf {r} ')\mathbf {s} (\mathbf {r} ')\rangle =}$

${\displaystyle =s(\mathbf {r} )g_{0}\mu _{B}\left(\mathbf {B} -{\frac {1}{g_{0}\mu _{B}}}\sum _{\mathbf {r} '}J(\mathbf {r} -\mathbf {r} ')\mathbf {\langle } s(\mathbf {r} ')\rangle \right)}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle g_{0},\mu _{B}}$ são, respectivamente o fator giromagnético e o magnéton de Bohr.

Substituindo o momento magnético:

${\displaystyle \mathbf {m} =-g_{0}\mu _{B}\mathbf {s} }$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

E o vetor magnetização:

${\displaystyle \mathbf {M} ={\frac {N}{V}}\langle \mathbf {m} \rangle }$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Tem-se:

${\displaystyle H_{magn}=-\mathbf {m} (\mathbf {r} )\left(\mathbf {B} +\sum _{\mathbf {r} '}{\frac {J(\mathbf {r} -\mathbf {r} ')}{(g_{0}\mu _{B})^{2}}}{\frac {V}{N}}\mathbf {M} \right)}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Logo:

${\displaystyle H_{magn}=-\mathbf {m} (\mathbf {r} )(\mathbf {B} +\lambda \mathbf {M} )}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Percebe-se uma analogia com o paramagnetismo de Langevin, no qual se faz o mesmo tipo de estudo, substituindo-se o campo magnético por um campo magnético eficaz, dado por:

${\displaystyle \mathbf {B} +\lambda \mathbf {M} }$.

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Existe, assim, uma temperatura crítica de Curie:

${\displaystyle T_{C}={\frac {J_{0}s(s+1)}{3k}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Abaixo da qual se manifestam os efeitos do ferromagnetismo. As quantidades “s” e “k” são os autovalores do spin e a constante de Boltzmann respectivamente, enquanto ${\displaystyle J_{0}}$ é dado por:

${\displaystyle \sum _{\mathbf {r} '}{\frac {J(\mathbf {r} -\mathbf {r} ')}{(g_{0}\mu _{B})^{2}}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A tensão elétrica de Planck é a unidade de tensão elétrica, notada por V_P, no sistema de unidades naturais conhecido como unidades de Planck.

${\displaystyle V_{P}={\frac {E_{P}}{q_{P}}}={\sqrt {\frac {c^{4}}{G4\pi \epsilon _{0}}}}\approx }$ 1.04295 × 10²⁷ V

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde

${\displaystyle E_{P}}$ é a energia de Planck

${\displaystyle q_{P}}$ é a carga de Planck

${\displaystyle c}$ é a velocidade da luz no vácuo

${\displaystyle G}$ é a constante gravitacional.

Em eletromagnetismo e em geometria diferencial, o tensor eletromagnético ou tensor campo eletromagnético (às vezes chamado de tensor de Faraday ou bivector de Maxwell) é um objeto matemático que descreve o campo eletromagnético de um sistema físico. O tensor de campo foi usado pela primeira vez após a formulação do tensor quadridimensional da relatividade especial e foi introduzido por Hermann Minkowski. O tensor permite que algumas leis físicas possam ser escritas de uma forma muito concisa.

Definição

O tensor electromagnético, convencionalmente marcado F, é definido como a derivada exterior do quadripotencial eletromagnético, A, um diferencial de forma 1:^[1][2]

${\displaystyle F\ {\stackrel {\mathrm {def} }{=}}\ \mathrm {d} A.}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em Eletrodinâmica e Eletromagnetismo, o teorema de Poynting expressa a lei da conservação da energia para o campo eletromagnético, sob a forma de uma equação diferencial parcial, estabelecida pelo físico britânico John Henry Poynting.^[1]

O teorema de Poynting é análogo ao teorema de trabalho e energia da mecânica clássica, e matematicamente semelhante à equação da continuidade, pois relaciona a energia armazenada no campo eletromagnético ao trabalho feito sobre uma distribuição de carga pelo campo elétrico, através do fluxo de energia por unidade de tempo.

Índice

• 1Definição
  • 1.1Geral
  • 1.2Engenharia Elétrica
• 2Verificação do Teorema
• 3Referências

Definição

Geral

Em palavras, o teorema é um balanço de energia^[2]:

A taxa de transferência de energia (por unidade de volume) a partir de uma região de espaço é igual à taxa de trabalho realizado(por unidade de tempo) sobre uma distribuição de carga, mais o fluxo de energia deixando essa região.

Relaciona a derivada temporal da densidade de energia eletromagnética com o fluxo de energia e a taxa em que o campo elétrico realiza um trabalho sobre uma distribuição de cargas.

Na forma diferencial, pode ser expressada pela fórmula:

                                              ${\displaystyle -{\frac {\partial u}{\partial t}}=\nabla \cdot {\vec {S}}+{\vec {J}}\cdot {\vec {E}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle \nabla \cdot {\vec {S}}}$ é a divergência do vetor de Poynting (fluxo de energia saindo da região), ${\displaystyle {\vec {J}}\cdot {\vec {E}}}$ o trabalho realizado pelo campo elétrico sobre uma distribuição de cargas (J é a Densidade de corrente livre devido ao movimento das cargas), e u é a energia armazenada no campo eletromagnético, dada pela formula:

                              ${\displaystyle u={\frac {1}{2}}\left({\vec {E}}\cdot {\vec {D}}+{\vec {B}}\cdot {\vec {H}}\right)={\frac {1}{2}}[\int _{V}\epsilon _{0}E^{2}dV+\int _{V}\mu _{0}H^{2}dV]}$ 

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

em que D é o deslocamento elétrico, S é o vetor de Poynting, B representa a densidade de fluxo magnético e H a intensidade de campo magnético.

A partir do teorema da divergência, o teorema de Poynting pode ser reescrito na forma integral:

                        ${\displaystyle {\frac {\partial }{\partial t}}\int _{V}{\frac {1}{2}}\epsilon _{0}E^{2}dV+{\frac {\partial }{\partial t}}\int _{V}{\frac {1}{2}}\mu _{0}H^{2}dV=-\oint _{A}({\vec {E}}\times {\vec {H}})\cdot d{\vec {A}}-\int _{V}{\vec {J}}\cdot {\vec {E}}dV}$ 

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle {\vec {E}}\times {\vec {H}}}$.é o vetor de Poynting instantâneo, ${\displaystyle \mu _{0}}$ e ${\displaystyle \epsilon _{0}}$ são as constantes de permeabilidades magnética e elétrica do vácuo respectivamente.

Engenharia Elétrica

Do ponto de vista da engenharia elétrica, o teorema geralmente é escrito com o termo densidade de energia eletromagnética ${\displaystyle u}$ ampliado, de forma que se assemelha à equação da continuidade:

                                     ${\displaystyle \nabla \cdot {\vec {S}}+\epsilon _{0}{\vec {E}}\cdot {\frac {\partial {\vec {E}}}{\partial t}}+{\frac {\vec {B}}{\mu _{0}}}\cdot {\frac {\partial {\vec {B}}}{\partial t}}+{\vec {J}}\cdot {\vec {E}}=0}$ 

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde:

• ${\displaystyle \epsilon _{0}}$ é a permissividade elétrica do vácuo;
• ${\displaystyle \mu _{0}}$ é a permeabilidade magnética do vácuo;
• ${\displaystyle \epsilon _{0}{\vec {E}}\cdot {\frac {\partial {\vec {E}}}{\partial t}}}$  ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  é a potência reativa acumulada no campo elétrico;
• ${\displaystyle {\frac {\vec {B}}{\mu _{0}}}\cdot {\frac {\partial {\vec {B}}}{\partial t}}}$ ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  é a potência reativa acumulada no campo magnético;
• ${\displaystyle {\vec {J}}\cdot {\vec {E}}}$ representa a densidade de energia elétrica dissipada pela força de Lorentz agindo sobre distribuições de carga.

Verificação do Teorema

Usando o teorema na forma integral, é simples demonstrar a validade do mesmo em um fio circulando uma corrente contínua.^[3]

Considere uma corrente ${\displaystyle I}$ contínua em um comprimento ${\displaystyle L}$ de um fio de raio ${\displaystyle a}$. Agora, considerando que os campos elétrico e magnético não variam com o tempo, a taxa de variação da energia armazenada nos mesmos é igual a zero, portanto:

(a) Uma corrente contínua, fluindo na direção +z em um fio de raio a. (b) Seção transversal do fio mostrando a orientação dos campos e o vetor de Poynting instantâneo na superfície do fio.

${\displaystyle \oint _{A}({\vec {E}}\times {\vec {H}})\cdot d{\vec {A}}=-\int _{V}{\vec {J}}\cdot {\vec {E}}dV}$ ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A corrente é assumida como estando uniformemente distribuída, de modo que a densidade de corrente seja:

${\displaystyle {\vec {J}}={\frac {I}{\pi a^{2}}}{\hat {z}}}$ ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

sendo ${\displaystyle {\hat {z}}}$ o vetor unitário apontando na direção +z.

Pela lei de Ohm, o campo elétrico é

${\displaystyle {\vec {E}}={\frac {\vec {J}}{\sigma }}={\frac {I}{\pi a^{2}\sigma }}{\hat {z}}}$ ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

sendo ${\displaystyle \sigma }$ a condutividade elétrica do fio.

No membro direito do teorema, usando coordenadas cilíndricas, temos:

${\displaystyle -\int _{V}{\vec {J}}\cdot {\vec {E}}dV=-{\frac {I^{2}}{\sigma (\pi a^{2})^{2}}}\int _{0}^{2\pi }\int _{0}^{a}\int _{0}^{L}rdzdrd\theta =-I^{2}{\frac {L}{\sigma \pi a^{2}}}=-I^{2}R}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

No membro da esquerda, precisamos de H. Aplicando a lei de Ampère, podemos determinar H na superfície do fio como sendo

${\displaystyle {\vec {H}}={\frac {I}{2\pi a}}{\hat {\theta }}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

sendo ${\displaystyle {\hat {\theta }}}$ o vetor unitário na direção tangente ao fio.

O vetor de poynting instantâneo é:

${\displaystyle {\vec {P}}={\vec {E}}\times {\vec {H}}={\frac {I}{\sigma \pi a^{2}}}{\hat {z}}\times {\frac {I}{2\pi a}}{\hat {\theta }}}$ ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle {\vec {P}}={\frac {I^{2}}{2\pi ^{2}a^{3}\sigma }}{\hat {r}}}$ ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

sendo ${\displaystyle {\hat {r}}}$ o vetor unitário na direção radial do fio.

O vetor ${\displaystyle {\vec {P}}}$ está direcionado radialmente para o interior do fio. Integrando sobre a superfície, temos:

${\displaystyle \oint _{A}({\vec {E}}\times {\vec {H}})\cdot {\vec {dA}}=\oint _{A}{\vec {P}}\cdot {\vec {dA}}=-{\frac {I^{2}a}{2\pi ^{2}\sigma a^{3}}}\int _{0}^{2\pi }\int _{0}^{L}dzd\theta =-I^{2}{\frac {L}{\sigma \pi a^{2}}}=-I^{2}R}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Esta parte do teorema diz que ${\displaystyle -I^{2}R}$ é a potência fluindo para fora do fio.

Aplicando esses valores no teorema, temos

${\displaystyle \oint _{A}({\vec {E}}\times {\vec {H}})\cdot {\vec {dA}}=-\int _{V}{\vec {J}}\cdot {\vec {E}}dV}$

${\displaystyle -I^{2}R=-I^{2}R}$ ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Logo, se não há uma variação na energia armazenada no campo eletromagnético que flui nessa região, a potência que flui para fora dessa região do fio é dissipada na forma de trabalho sobre as cargas por efeito joule.

Vetor potencial magnético ou potencial do vetor magnético^[1][2], A, é a grandeza vetorial no eletromagnetismo clássico definida de modo que sua curva seja igual ao campo magnético: ${\textstyle \nabla \times \mathbf {A} =\mathbf {B} \,}$.^[3] Junto com o potencial elétrico φ, o potencial do vetor magnético pode ser usado para especificar também o campo elétrico E. Portanto, muitas equações do eletromagnetismo podem ser escritas em termos de campos E e B, ou de forma equivalente em termos dos potenciais φ e A.^[4] Em teorias mais avançadas, como a mecânica quântica, a maioria das equações usa potenciais em vez de campos. Historicamente, Lord Kelvin introduziu pela primeira vez o potencial vetorial em 1851, junto com a fórmula que o relaciona com o campo magnético.^[5]

Índice

• 1Potencial do vetor
  • 1.1Opções de medidor
  • 1.2Equações de Maxwell em termos de potencial vetorial
  • 1.3Cálculo de potenciais de distribuições de fonte
  • 1.4Representação do campo A
  • 1.5Quatro potenciais eletromagnéticos
• 2Veja também
• 3Referências
• 4Bibliografia

Potencial do vetor

O potencial do vetor magnético A é um campo vetorial, definido junto com o potencial elétrico ϕ (um campo escalar) pelas equações:^[6]

${\displaystyle \mathbf {B} =\nabla \times \mathbf {A} \,,\quad \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}\,,}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde B é o campo magnético e E é o campo elétrico. Em magnetostática, onde não há distribuição de carga variável no tempo, apenas a primeira equação é necessária. (No contexto da eletrodinâmica, os termos potencial vetorial e potencial escalar são usados ​​para o potencial vetorial magnético e potencial elétrico, respectivamente. Em matemática, o potencial vetorial e o potencial escalar podem ser generalizados para dimensões superiores.)

Se os campos elétricos e magnéticos são definidos como acima a partir dos potenciais, eles satisfazem automaticamente duas das equações de Maxwell: a lei de Gauss para o magnetismo e a lei de Faraday. Por exemplo, se A é contínuo e bem definido em todos os lugares, então é garantido que não resultará em monopólos magnéticos. (Na teoria matemática dos monopólos magnéticos, A pode ser indefinido ou com valores múltiplos em alguns lugares; veja monopolo magnético para detalhes).

Começando com as definições acima:

${\displaystyle {\begin{aligned}\nabla \cdot \mathbf {B} &=\nabla \cdot \left(\nabla \times \mathbf {A} \right)=0\\\nabla \times \mathbf {E} &=\nabla \times \left(-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}\right)=-{\frac {\partial }{\partial t}}\left(\nabla \times \mathbf {A} \right)=-{\frac {\partial \mathbf {B} }{\partial t}}.\end{aligned}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Alternativamente, a existência de A e ϕ é garantido a partir dessas duas leis usando o teorema de Helmholtz. Por exemplo, uma vez que o campo magnético é livre de divergência (lei de Gauss para o magnetismo; ou seja, ∇ ⋅ B = 0), sempre existe um A que satisfaz a definição acima.

O potencial do vetor Aé usado ao estudar o Lagrangiano na mecânica clássica e na mecânica quântica (veja a equação de Schrödinger para partículas carregadas, equação de Dirac e efeito Aharonov-Bohm).

No sistema SI, as unidades de A são V·s·m⁻¹ e são iguais ao momento por unidade de carga, ou força por unidade de corrente. No acoplamento mínimo, qA é chamado de momento potencial e faz parte do momento canônico.

A integral de linha de A sobre um "loop" fechado é igual ao fluxo magnético através da superfície fechada:

${\displaystyle \oint _{\Gamma }\mathbf {A} \,\cdot \,d{\mathbf {\Gamma } }=\iint _{S}\nabla \times \mathbf {A} \,\cdot \,d\mathbf {S} =\Phi _{B}.}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Portanto, as unidades de A também são equivalentes a Weber por metro . A equação acima é útil na quantização de fluxo de loops supercondutores .

Embora o campo magnético B seja um pseudovetor (também chamado de vetor axial ), o potencial vetorial A é um vetor polar .^[7] Isso significa que se a regra da mão direita para produto vetorial fosse substituída por uma regra da mão esquerda, mas sem alterar nenhuma outra equação ou definição, então B trocaria de sinal, mas A não mudaria. Este é um exemplo de um teorema geral: a curva de um vetor polar é um pseudovetor e vice-versa.

Opções de medidor

A definição acima não define o potencial do vetor magnético exclusivamente porque, por definição, podemos adicionar arbitrariamente componentes livre de onda para o potencial magnético sem alterar o campo magnético observado. Portanto, há um certo grau de liberdade disponível ao escolher A. Esta condição é conhecida como invariância de calibre .

Equações de Maxwell em termos de potencial vetorial

Usar a definição de potenciais acima e aplicá-la às outras duas equações de Maxwell (aquelas que podem parecer mais estranhas) resulta em uma equação diferencial complicada que pode ser simplificada usando o medidor de Lorenz onde A é escolhido para satisfazer:

${\displaystyle \nabla \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}=0.}$ ^[6]

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Usando o medidor de Lorenz, as equações de Maxwell podem ser escritas compactamente em termos do potencial vetorial magnético A e do potencial escalar elétrico ϕ :^[6]

${\displaystyle {\begin{aligned}\nabla ^{2}\phi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\phi }{\partial t^{2}}}&=-{\frac {\rho }{\epsilon _{0}}}\\\nabla ^{2}\mathbf {A} -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}&=-\mu _{0}\mathbf {J} \end{aligned}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em outros medidores, as equações são diferentes. Uma notação diferente para escrever essas mesmas equações (usando quatro vetores ) é mostrada abaixo.

Cálculo de potenciais de distribuições de fonte

As soluções das equações de Maxwell no medidor de Lorenz (ver Feynman ^[6] e Jackson ^[8] ) com a condição de contorno de que ambos os potenciais vão a zero suficientemente rápido à medida que se aproximam do infinito são chamadas de potenciais retardadores, que são o potencial do vetor magnético A(r, t) e o potencial escalar elétrico ϕ(r, t) devido a uma distribuição de corrente de densidade de corrente J(r′, t′), densidade de carga ρ(r′, t′), e volume Ω, dentro do qual ρ e J são diferentes de zero (pelo menos às vezes e em alguns lugares):

${\displaystyle {\begin{aligned}\mathbf {A} \left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {\mathbf {J} \left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\\\phi \left(\mathbf {r} ,t\right)&={\frac {1}{4\pi \epsilon _{0}}}\int _{\Omega }{\frac {\rho \left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\end{aligned}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde os campos no vetor posição r e tempo t são calculados a partir de fontes na posição distante r' em um tempo anterior t'. A localização r ′ é um ponto fonte na distribuição de carga ou corrente (também a variável de integração, dentro do volume Ω ). O tempo anterior t ′ é chamado de tempo retardado e calculado como

${\displaystyle t'=t-{\frac {\left|\mathbf {r} -\mathbf {r} '\right|}{c}}}$ .

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Existem algumas coisas notáveis sobre A e ϕ calculados desta forma:

• (A condição do medidor Lorenz ): ${\displaystyle \nabla \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}=0}$  ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  é satisfeito.
• A posição de r, o ponto em que os valores de ϕ e A são encontrados, só entra na equação como parte da distância escalar de r ′ a r . A direção de r ′ para r não entra na equação. A única coisa que importa sobre um ponto de origem é a distância dele.
• O integrando usa o tempo retardado, t ′. Isso simplesmente reflete o fato de que as mudanças nas fontes se propagam na velocidade da luz. Conseqüentemente, as densidades de carga e corrente que afetam o potencial elétrico e magnético em r e t, da localização remota r', também devem estar em algum tempo anterior t ′.
• A equação para A é uma equação vetorial. Em coordenadas cartesianas, a equação se separa em três equações escalares:^[9]

  ${\displaystyle {\begin{aligned}A_{x}\left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {J_{x}\left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\\A_{y}\left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {J_{y}\left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\\A_{z}\left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {J_{z}\left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\end{aligned}}}$

   ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Dessa forma, é fácil ver que o componente de A em uma dada direção depende apenas dos componentes de J que estão na mesma direção. Se a corrente for conduzida por um fio longo e reto, A aponta na mesma direção do fio.

Em outros medidores, a fórmula para A e ϕ é diferente.(Consulte o medidor de Coulomb para uma outra possibilidade.

Representação do campo A

Representando o po tencial de vetor magnético de calibre Coulomb A, a densidade de fluxo magnético B e os campos de densidade de corrente J em torno de um indutor toroidal de seção transversal circular. Linhas mais grossas indicam linhas de campo de maior intensidade média. Os círculos na seção transversal do núcleo representam o campo B saindo da imagem, mais os sinais representam o campo B entrando na imagem. ∇ ⋅ A = 0 foi assumido.

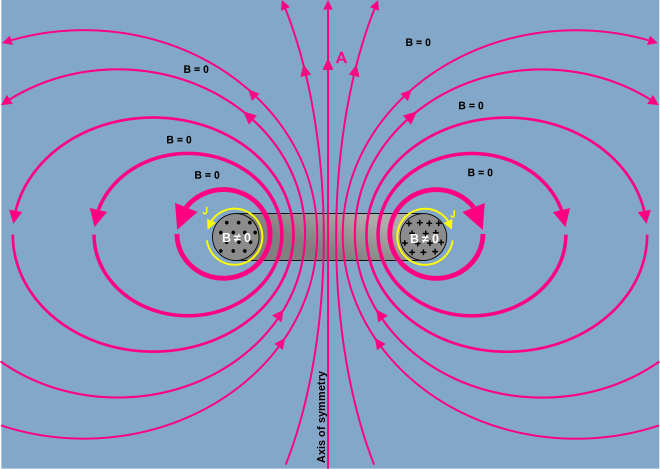
Veja Feynman ^[10] para a representação do campo A em torno de um solenoide longo e fino.

Desde a

${\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {J} }$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

assumindo condições quase estáticas, ou seja,

${\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0\,\quad \nabla \times \mathbf {A} =\mathbf {B} \,,}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

as linhas e contornos de A se relacionam com B como as linhas e contornos de B se relacionam com j . Assim, uma representação do campo A em torno de um loop de fluxo B (como seria produzido em um indutor toroidal ) é qualitativamente o mesmo que o campo B em torno de um loop de corrente.

A figura à direita é a representação artística do campo A. As linhas mais grossas indicam caminhos de intensidade média mais alta (caminhos mais curtos têm intensidade mais alta, de modo que a integral do caminho é a mesma). As linhas são desenhadas para (esteticamente) transmitir a aparência geral do A longe.

O desenho tacitamente assume ∇ ⋅ A = 0, verdadeiro sob uma das seguintes suposições:

• o medidor de Coulomb é assumido
• o medidor de Lorenz é assumido e não há distribuição de carga, ρ = 0 ,
• o medidor Lorenz é assumido e a frequência zero é assumida
• o medidor Lorenz é assumido e uma frequência diferente de zero que é baixa o suficiente para negligenciar ${\displaystyle {\frac {1}{c}}{\frac {\partial \phi }{\partial t}}}$ é assumido.

•  ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Quatro potenciais eletromagnéticos

No contexto da relatividade especial, é natural juntar o potencial vetorial magnético com o potencial elétrico (escalar) no potencial eletromagnético, também chamado de quatro potenciais .

Uma motivação para fazer isso é que o quatro potenciais é um quadrivetor matemáticos. Assim, usando regras de transformação de quatro vetores padrão, se os potenciais elétricos e magnéticos são conhecidos em um referencial inercial, eles podem ser simplesmente calculados em qualquer outro referencial inercial.

Outra motivação relacionada é que o conteúdo do eletromagnetismo clássico pode ser escrito de uma forma resumida e conveniente usando o potencial eletromagnético quatro, especialmente quando o medidor de Lorenz é usado. Em particular, na notação de índice abstratos, o conjunto de equações de Maxwell (no calibre de Lorenz) pode ser escrito (em unidades gaussianas ) como segue:

${\displaystyle {\begin{aligned}\partial ^{\mu }A_{\mu }&=0\\\Box A_{\mu }&={\frac {4\pi }{c}}J_{\mu }\end{aligned}}}$

 ///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde □ é o Operador de d'Alembert e J é a quatro correntes . A primeira equação é a condição de medidor de Lorenz, enquanto a segunda contém as equações de Maxwell. Os quatro potenciais também desempenham um papel muito importante na eletrodinâmica quântica .